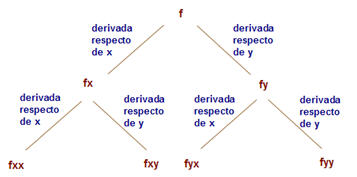
Si f es una función de dos variables, entonces sus derivadas parciales también son funciones de dos variables, de modo que podemos considerar a sus derivadas parciales, las cuales se llaman segundas derivadas parciales de f.
Así, si f:D⊆ ℝ 2 →ℝ es una función de dos variables que tiene derivadas parciales respecto de x y de y en todos los puntos de D, quedan definidas dos nuevas funciones f x , f y :D⊆ ℝ 2 →ℝ .
Si las derivadas parciales de estas funciones existen se pueden definir las derivadas parciales de orden 2.
Teorema de Young
Este teorema afirma que si z=f(x,y) y f es continua en un punto P(x,y) y las derivadas parciales de primer orden son continuas en el punto P, entonces se cumple que:
(∂2f/ ∂x
∂y)= (∂2f/ ∂y ∂x)
No hay comentarios:
Publicar un comentario